در این بخش به آموزش تابع بازگشتی در زبان C، خواهیم پرداخت. یکی از مهمترین مفاهیم علم کامپیوتر، توابع بازگشتی هستند که کاربرد بسیار زیادی در حل مسائل دارند. به طور کلی منظور از توابع بازگشتی، عملیاتی است که تولید خروجی برای هر مقداری، نتیجه فرمولی یکسان روی مقادیری از جملات قبلی آن باشد. توابع بازگشتی توابعی هستند که در درون تعریف خود تابع هم فراخوانی میشوند. هدف از اینکار صرفه جویی در کد نویسی و ایجاد خلاقیت است.
۱- توابع درون برنامه ای
فراخوانی یک تابع دارای سربار زمانی و حافظه ای می باشد. با فراخوانی هر تابع باید برای متغیرهای محلی و پارامترهای آن حافظه تخصیص داده شود، آرگومانهای ارسالی در پارامترهای تابع کپی شوند و … که همگی این موارد باعث صرف زمان و حافظه می شوند. به همین دلیل برای انجام عملیات کوتاه، استفاده از تابع ایده چندان خوبی نیست؛ چراکه گرچه خوانایی برنامه بالا می رود، اما برای انجام یک کار کوچک، هزینه زیادی به سیستم تحمیل می گردد. برای رفع این مشکل، زبان C از توابع درون برنامه ای یا inline استفاده می آند. اگر قبل از شروع تعریف تابع (یعنی قبل از نوع مقدار بازگشتی) از کلمه کلیدی inline استفاده شود، به کامپایلر توصیه می شود که هر فراخوانی تابع مورد نظر را با یک کپی صریح از کد تابع جایگزین نماید، تا دیگر نیازی به صرف زمان برای فراخوانی تابع نباشد. بعنوان مثال به نمونه زیر دقت کنید:
inline int square(int n) {
return (n*n) ;
}
void main() {
int a, b ;
a = square(5) ;
b = square(2*a+3) ;}
در اینحالت کامپایلر تابع main را بصورت زیر تغییر می دهد:
void main() {
int a,b ;
a = (5) * (5) ;
b = (2*a+3) * (2*a+3) ;
}
البته استفاده از، inline گرچه باعث بالا رفتن سرعت اجرای برنامه می شود، اما حجم آن را بالا می برد؛ چرا که بجای هر فراخوانی تابع، یک کپی از آن را قرار می دهد. در نتیجه استفاده از این مشخصه، فقط در توابع کوچک قابل قبول است. در حقیقت C از این مشخصه برای توابع بزرگ صرفنظر می کند.
۲- توابع بازگشتی
یکی از مهمترین مفاهیم علم کامپیوتر، توابع بازگشتی هستند که کاربرد بسیار زیادی در حل مسائل دارند. توابع بازگشتی، توابعی هستند که خود را مجددا فراخوانی می کنند. این توابع به دو دسته تقسیم می شوند:
- توابع بازگشتی مستقیم : تابعی مانند ،Aخودش را فراخوانی نماید.
- توابع بازگشتی غیر مستقیم : تابعی مانند A تابع دیگری مانند Bرا فراخوانی نماید و سپس B مجددا تابع A را فراخوانی نماید.
ما در این آموزش توابع بازگشتی، منحصرا به بررسی توابع بازگشتی مستقیم خواهیم پرداخت.
اما چرا یک تابع باید خودش را فراخوانی نماید؟ در بعضی مسائل که عموما مسائل پیچیده ای نیز هستند می توان یک نمونه از مسئله را با استفاده از نمونه ساده تر یا کوچکتری از همان مسئله حل کرد. بنابراین، تابع می تواند برای حل مسئله بزرگتر، نسخه جدیدی از خودش را برای حل مسئله کوچکتر فراخوانی نماید و سپس با استفاده از نتایج بدست آمده، مسئله بزرگ را حل نماید. مسلم است که تابعی که برای حل مسئله کوچک فراخوانی شده است نیز از همین مکانیزم استفاده کرده و مجددا خودش را برای حل یک مسئله کوچکتر فراخوانی خواهد کرد. اما این فراخوانیها تا چه زمانی ادامه پیدا می آند؟ هر مسئله بازگشتی دارای یک حالت پایه است که حل آن بدیهی بوده و نیازی به حل یک مسئله کوچکتر ندارد. بنابراین تابع بازگشتی حتما باید دارای یک شرط برای بررسی حالت پایه باشد، که به آن شرط توقف گفته می شود. هنگامی که تابع به حالت پایه می رسد، فراخوانی بازگشتی را متوقف کرده و حل بدیهی مسئله را برای فراخوانی قبلی تابع باز می گرداند. سپس این بازگرداندن مقادیر رو به عقب تکرار می شود تا هنگامی که به نسخه اولیه تابع برسد و در نهایت جواب نهایی به تابع اصلی بازگردانده شود.
اکنون برای روشن شدن موضوع به بررسی یک مثال آلاسیک در زمینه توابع بازگشتی، یعنی محاسبه فاکتوریال می پردازیم. قبلا نحوه محاسبه فاکتوریال یک عدد را بصورت زیر بیان کردیم :
n! = 1 × ۲ × … × n
تابع مربوط به فاکتوریال نیز با استفاده از یک حلقه تکرار آه اعداد ۱تا nرا در یکدیگر ضرب می کرد، نوشته شد. اما اگر به تعریف فاکتوریال دقت آنیم، درمی یابیم که فاکتوریال عددی مانند ۵ را می توان از ضرب عدد ۵در فاکتوریال ۴ بدست آورد. بطور کلی می توان گفت:
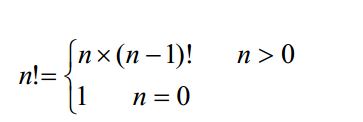همانطور که دیده می شود، حالت پایه در این مسئله، حالت n=0 است؛ چرا که در این حالت حل مسئله بدیهی بوده و جواب برابر یک است.
*تابع بازگشتی فاکتوریال بصورت زیر نوشته می شود:
long int factorial(int n) {if (n ==0) return(1) ;
else return(n * factorial(n-1));
}
همانطور که دیده می شود، توابع باز گشتی بسیار ساده و کوچک می باشند، اما درک نحوه کار آنها کمی مشکل است. قبل از توضیح نحوه کار این تابع، توجهکنید که هنگامیکه یک تابع خودش را فراخوانی می کند، یک نسخه جدید از آن تابع بوجود می آید. بدین معنا که یک نسخه جدید از کلیه پارامترها و متغیرهای محلی تابع ایجاد می شود و عملیات برروی این متغیرهای جدید انجام می شود. بدون اینکه تغییری در متغیرهای فراخوانی قبلی ایجاد شود. البته برای صرفه جویی در حافظه، نسخه جدیدی از دستورات برنامه ایجاد نمی شود.
شکل زیر نحوه انجام عملیات را برای فراخوانی (factorial(4 نشان می دهد. اعداد روی فلشها، مقدار ارسالی به تابع و یا مقدار بازگشتی از تابع رانشان می دهند، و اعداد داخل دایره، ترتیب فراخوانی و بازگشت را مشخص می نمایند.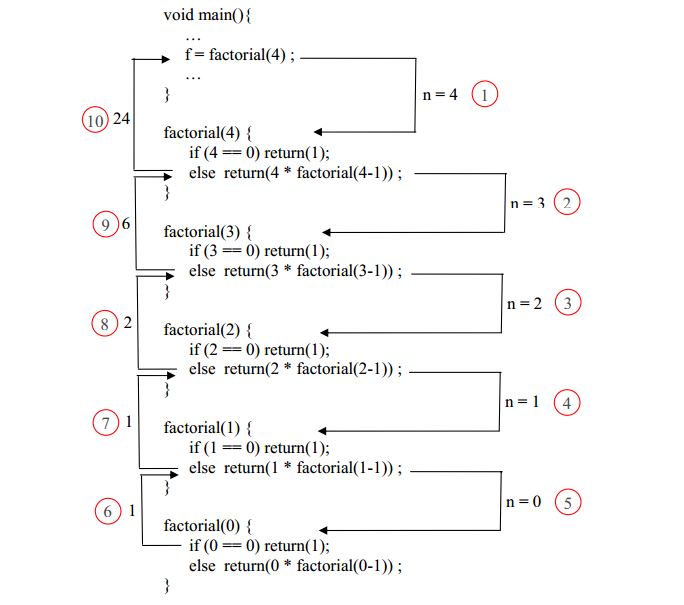 
همانطور که دیده می شود، دنبال کردن نحوه کار توابع بازگشتی قدری دشوار است و بهمین دلیل، اشکال زدایی آنها نیز نسبتا مشکل است. اما معمولا خود توابع ساده تر و واضح تر از نمونه غیر بازگشتی خود هستند. روش دیگری نیز برای دنبال کردن توابع باز گشتی وجود دارد. در این روش هر بار فراخوانی تابع، با یک مستطیل نشان داده می شود که در داخل کن مقادیر پارامترها و متغیرهای محلی و همچنین مقادیر بازگشتی تابع نوشته می شود. هر بار فراخوانی مجدد با یک فلش به مستطیل بعدی نشان داده می شود و در هنگام بازگشت نیز یک فلش به مستطیل قبلی رسم می شود. این روش به افراد کمک می کند مقادیر متغیرهای محلی و پارامترها را در حین فراخوانیهای متعدد مشاهده نمایند. به مثال زیر توجه کنید:
*تابعی بنویسید که دو عدد را دریافت و بزرگترین مقسوم علیه مشترک آن دو را بازگرداند:
int gcd(int x, int y) {
if (y == 0) return(x);
else return( gcd(y, x%y) );
}
مقایسه روشهای تکراری و توابع بازگشتی
همانطور که قبلا دیده شد، الگوریتم فاکتوریال را می توان به دوصورت تکراری با حلقه تکرار و بازگشتی نوشت. آیا این مسئله برای سایر الگوریتمهای بازگشتی نیز برقرار است؟ جواب مثبت است. هر الگوریتم بازگشتی را می توان بصورت غیر بازگشتی یا تکراری نیز نوشت، گرچه ممکن است راه حل کن پیچیده تر و وضوح آن نیز کمتر باشد. اما کدام روش بهتر است؟
همانطور که دیدید، در الگوریتمهای بازگشتی، با هربار فراخوانی تابع یک نسخه جدید از متغیرها ایجاد می شود. به همین دلیل معمولا الگوریتمهای بازگشتی حافظه بیشتری را نسبت به الگوریتمهای تکراری مصرف می نمایند. علاوه براین الگوریتمهای بازگشتی معمولا از نظر زمان اجرا نیز کندتر هستند. دلیل این مسئله سربار ناشی از فراخوانی مکرر تابع است. هربار فراخوانی یک تابع، باعث می شود که عملیات خاصی همانند ذخیره آدرس برگشت از تابع انجام گیرد که سربار زمانی کمی را ایجاد می کند. اما فراخوانیهای متعدد، باعث ایجاد سربار زمانی قابل توجهی می گردد.با توجه به این نکات منفی، چرا از توابع بازگشتی استفاده کنیم؟
نکته: تنها هنگامی از توابع بازگشتی استفاده نماییدکه طبیعت مساله بگونه ای باشد که توسط روشهای بازگشتی راحتتر حل شود و الگوریتم حاصل ساده تر و واضحتر باشد. در بسیاری از مسائل، روش بازگشتی بسیار ساده و آسان بوده و درک و اشکال زدایی آن بسیار ساده است، درحالیکه راه حل غیربازگشتی به راحتی به ذهن نمی رسد و یا بسیار پیچیده است. اما در مواردی که کارایی اهمیت زیادی دارد، هرگز از بازگشت استفاده ننمایید.
