
الگوریتم جستجوی دودویی (Binary Search)
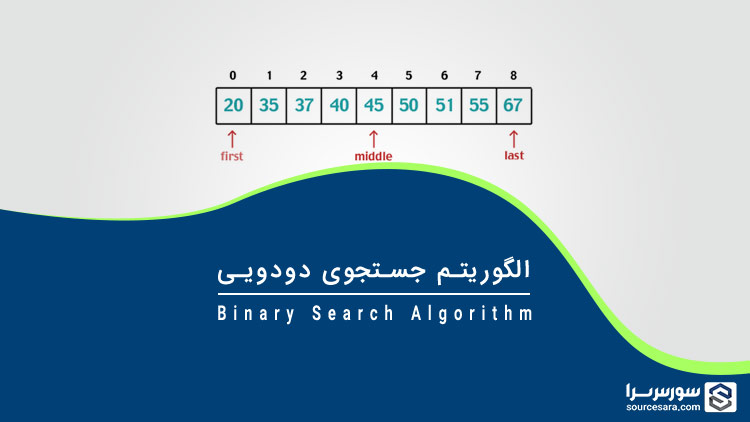
الگوریتم جستجوی دودویی (Binary Search) در هر گام از جستجو محدوده جستجو را به نصف کاهش می دهد. روش کار به این صورت است که ابتدا عنصر مورد نظر با عنصر خانه وسط مقایسه می شود، اگر با مقدار این خانه برابر بود (بهترین حالت) جستجو تمام می شود. اگر مقدار عنصر مورد نظر از مقدار عنصر خانه وسط بزرگتر بود، بخش بالایی به دو قسمت تقسیم می شود و جستجو در بخش بالایی آرایه ادامه می یابد. اما اگر مقدارش از مقدار عنصر خانه وسط کوچکتر بود، بخش پایینی به دو قسمت تقسیم می شود و جستجو در بخش پایینی آرایه ادامه پیدا می کند. این عملیات تا زمانی که همه عناصر آرایه بررسی شوند، یا عنصر مورد نظر پیدا شود، ادامه می یابد.

مسئله
با توجه به آرایه مرتب داده شده (arr[])، تابعی بنویسید که عنصر x را در آرایه جستجو کند.
مثال
راه حل ساده برای حل این مسئله استفاده از الگوریتم جستجوی خطی (linear search) خطی با پیچدگی زمانی O(n) است. یک راه حل دیگر برای این مسئله استفاده از الگوریتم جستجوی باینری (binary search) است. پیچیدگی زمانی الگوریتم باینری سرچ، O(Log n) است و فقط در آرایه های مرتب شده می تواند مورد استفاده قرار گیرد.
حل
در این الگوریتم فقط با یک مقایسه، نصف آرایه از محدوده جستجو خارج می شود.
- مقایسه x با عنصر وسط آرایه.
- اگر مقدار x و عنصر وسط برابر بود، اندیس آن بازگردانده می شود.
- در غیر این صورت، اگر مقدار x از مقدار عنصر وسط بزرگتر باشد، یعنی x در صورت وجود داشتن، در بخش بالایی است. بنابراین در گام بعدی بخش بالایی جستجو می شود.
- اما اگر x کوچکتر از عنصر وسط باشد، بخش پایینی جستجوی می شود.
- اگر x پیدا نشود، مقدار -۱ بازگردانده می شود.
پیاده سازی الگوریتم جستجوی دودویی به صورت بازگشتی:
// C program to implement recursive Binary Search
#include <stdio.h>
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not
// present in array
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? printf("Element is not present in array")
: printf("Element is present at index %d",
result);
return 0;
}
امتحان کنید
خروجی:
Element is present at index 3
پیاده سازی الگوریتم جستجوی باینری به صورت عادی (حلقه while):
// C program to implement iterative Binary Search
#include <stdio.h>
// A iterative binary search function. It returns
// location of x in given array arr[l..r] if present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
while (l <= r) {
int m = l + (r - l) / 2;
// Check if x is present at mid
if (arr[m] == x)
return m;
// If x greater, ignore left half
if (arr[m] < x)
l = m + 1;
// If x is smaller, ignore right half
else
r = m - 1;
}
// if we reach here, then element was
// not present
return -1;
}
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? printf("Element is not present"
" in array")
: printf("Element is present at "
"index %d",
result);
return 0;
}
امتحان کنید
خروجی:
Element is present at index 3
پیچدگی زمانی
پیچدگی زمامی الگوریتم جستجوی باینری را می توان به شکل زیر نوشت:
T(n) = T(n/2) + c
نوشته الگوریتم جستجوی دودویی (Binary Search) اولین بار در سورس سرا - آموزش برنامه نویسی. پدیدار شد.